The concept of “Infinity” always intrigued humanity and has been the subject of study by many scholars and philosophers throughout human civilization. Historically, debates about infinity predate Plato and Aristotle and were a constant in the schools of Greek thought. However, due to their complexity, they were avoided until the Renaissance, in the fifteenth century, when the discussion about infinity resurfaced, but which was only thoroughly studied during the nineteenth and twentieth century.

In nature, an intriguing species of jellyfish seems to have found a way to become eternal, managing to evade natural death. In general, jellyfish undergo rapid aging after reaching sexual maturity and reproducing, but not Turritopsis Nutricula.

According to scientists, if subjected to stress conditions and great danger, members of the species have the ability to spontaneously reverse their adult condition back to the way they were when they were young, essentially the first stage of the life cycle of the jellyfish species (which is a polyp, or a fixed tube with anemone like tentacles). The species changes its existing cells, which can replicate and mutate into other cells when adults again, like human stem cells.

After reverting to their younger condition, jellyfish return to the adult form, and the process can be repeated infinitely. Humans also have this capacity to renew, return to zero and start over. Companies often need to restructure, revise their strategy, renew and change.

Among the models of business formation, the Corporation is the one who best expresses the concept of infinity in human relations. By law, the duration of an association in the form of a Corporation can be “forever”. It has unlimited duration, since it is distinct from its owners, and the death or withdrawal of a shareholder does not affect the existence of the company; it can continue even after the withdrawal of its original owners. This concept should be reflected in the monetary valuation of a company, since it can generate perpetual returns, in other words, it can theoretically provide a perpetual source of profits.

In company valuation methodologies, the concept of Perpetuity is one of the components that most confuse readers of valuation reports and financial articles, especially regarding the calculation methods.

In the Discounted Cash Flow Methodology, the value of the company is composed of the present value of cash flows generated by the company, divided into two periods in the future: the period corresponding to the long-term planning of the company, i.e., typically 5 to 10 years and the period of perpetuity. As the generation of cash for a company is theoretically infinite and, therefore, part of the enterprise value, referred to as the value of perpetuity, it will be generated by a constant series of cash flows from the years following the last year of its long term planning period. To get an idea, in some cases, the value of perpetuity may represent the largest portion of the total value of the company, (Enterprise Value). It can be a difficult task for some people to abstract a concept as ethereal as the concept of eternity and turn it into a simple mathematical calculation, especially for those who wish to acquire a company (or any asset) and pay a significant portion of value for this.

In general, the formula for the Present Value of a series of limited cash flows corresponds to::

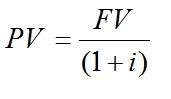
Thus, the formula for the present value of perpetual cash would be the sum of infinite terms of the present value formula expressed above. Thus, calculating countless “Present Values” would be impractical for an infinitely long series. The series, as presented above, are called Geometric Progressions, which despite having an infinitely large number of terms have a finite sum.

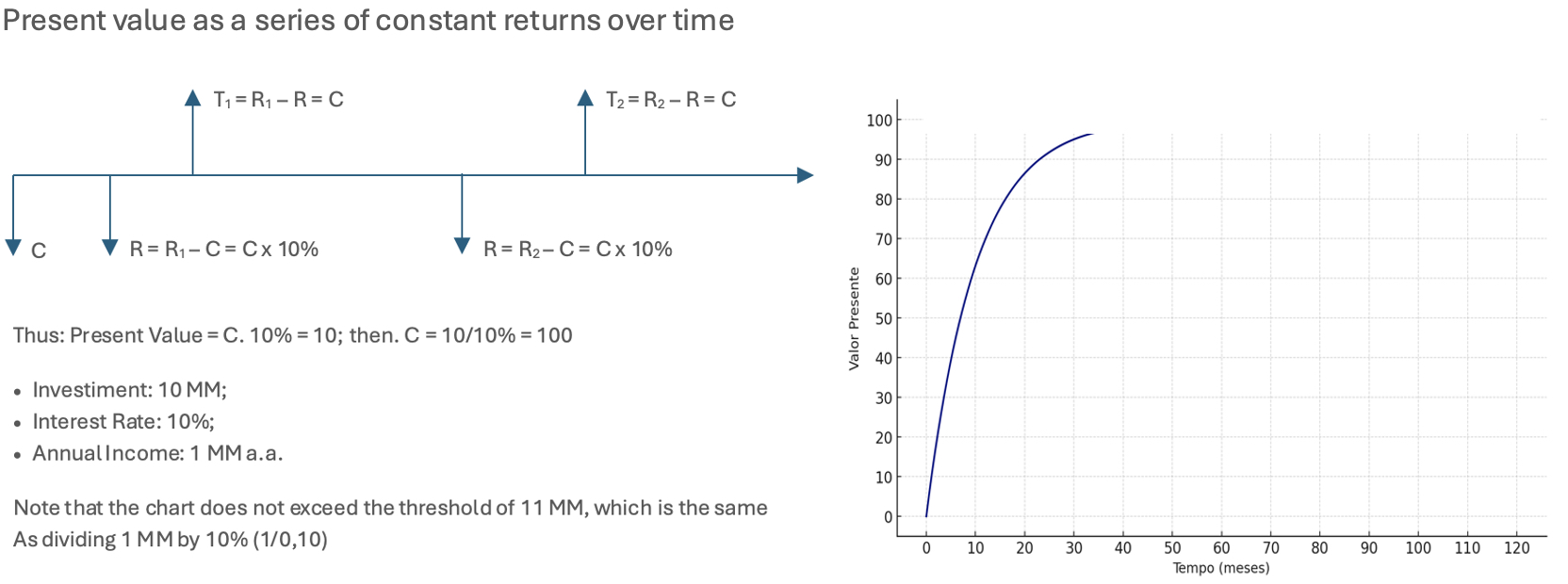
Nevertheless, the calculation of perpetuity can be easily understood intuitively by means of a chart, or algebraically. Imagine an investment C, which will yield R income annually, and that the investor wants to take from his investment, annually, the value of R. Now, let’s say the investor knows he intends to withdraw annually 1 MM and the interest rate on the investment is 10%, how much would he need to invest to obtain R (R = 1 MM) annually?

As R = C x 10%, then C = R / 10%, therefore C is equal to 10 mm. Note that if we applied an amount equal to R / 10%, to income of 10%, we would see that the income would be equal to R, since: (R / 10%) x 10% = R.

In the projection of perpetuity, we see that the flows will be constant and equal, and only as such, would it be possible to apply the above. However, there are cases where the income in each period has constant growth. The idea is that the cash flow of the subsequent years (that makes up each year in perpetuity) will unlikely be without growth, given that there will at least be inflation. In such cases, the simplified formula for the present value of perpetuity is similar to the previous case, but inflation is subtracted from the rate of growth.

Thus, C = R / (10% (-) growth rate). Note that the growth rate cannot exceed the value of the discount rate, since the division would not be possible.

In cases of Mergers and Acquisitions, it is common for analysts, when using the Discounted Cash Flow methodology, to make the calculation of perpetuity, without neglecting the constant growth rate, which is at least the perpetual inflation rate, which corresponds to at least the projected inflation rate for the country in which the company operates.

If the reader thinks that perpetuities are irrelevant in reality, there is a well-known cash flow with infinite duration: the so-called British obligations referred to as consols. An investor who buys a consol is entitled to receive annual interest from the British government forever. A similar case was the issuance of U.S. bonds for the construction of the Panama Canal, but the U.S. government chose to repay the entire amount after some time. Preferred shares issued by companies in the stock market are another example: if there was no doubt that the company would actually pay the dividend for the preferred shares, such share would in fact be a consol.

Consolsare obligations that never stop paying a coupon, have no maturity date, and therefore never mature. Thus, a consol is a perpetuity. In the eighteenth century, the Bank of England, who held various debt securities, decided to consolidate such securities into only one, which became known as English consols. They were obligations, which according to the guarantee of the Bank of England, would give the bearer an infinite cash flow.

Vinicius Basilio (vinicius.basilio@camayapartners.com) is a partner of Camaya Partners.